In Drawing A Histogram, Which Of The Following Suggestions Should Be Followed?

Histograms are graphs that display the distribution of your continuous information. They are fantastic exploratory tools considering they reveal properties about your sample data in ways that summary statistics cannot. For instance, while the hateful and standard departure can numerically summarize your data, histograms bring your sample data to life.

In this weblog post, I'll show you how histograms reveal the shape of the distribution, its central trend, and the spread of values in your sample data. You'll also acquire how to identify outliers, how histograms relate to probability distribution functions, and why yous might need to use hypothesis tests with them.

Histograms, Key Tendency, and Variability

Use histograms when you have continuous measurements and want to understand the distribution of values and look for outliers. These graphs take your continuous measurements and place them into ranges of values known as bins. Each bin has a bar that represents the count or percentage of observations that fall within that bin. Histograms are similar to stalk and leaf plots.

Download the CSV data file to make most of the histograms in this blog mail service: Histograms.

In the field of statistics, nosotros often use summary statistics to describe an entire dataset. These statistics use a single number to quantify a characteristic of the sample. For case, a measure out of central tendency is a single value that represents the centre point or typical value of a dataset, such as the mean. A measure of variability is some other type of summary statistic that describes how spread out the values are in your dataset. The standard difference is a conventional mensurate of dispersion.

These summary statistics are crucial. How often have you heard that the mean of a group is a particular value? It provides meaningful information. However, these measures are simplifications of the dataset. Graphing the data brings it to life. Generally, I find that using graphs in conjunction with statistics provides the best of both worlds!

Let'south see this in action.

Related posts: Measures of Central Tendency, What is the Mean?, Measures of Variability and Using the Standard Departure.

Histograms and the Central Trend

Utilize histograms to empathize the eye of the data. In the histogram below, you can see that the center is near fifty. Nigh values in the dataset will be shut to 50, and values farther away are rarer. The distribution is roughly symmetric and the values fall betwixt approximately xl and 64.

A difference in means shifts the distributions horizontally along the Ten-axis (unless the histogram is rotated). In the histograms below, 1 group has a hateful of l while the other has a mean of 65.

Additionally, histograms help you grasp the degree of overlap between groups. In the to a higher place histograms, there's a relatively modest amount of overlap.

Histograms and Variability

Suppose yous hear that ii groups accept the same hateful of l. It sounds like they're practically equivalent. However, after you graph the data, the differences get apparent, as shown below.

The histograms center on the same value of 50, but the spread of values is notably different. The values for group A mostly autumn between forty – 60 while for group B that range is xx – 90. The hateful does not tell the entire story! At a glance, the difference is evident in the histograms.

In short, histograms show yous which values are more and less common along with their dispersion. Yous can't proceeds this understanding from the raw listing of values. Summary statistics, such as the mean and standard deviation, will get you partway in that location. But histograms make the data pop!

Histograms and Skewed Distributions

Histograms are an fantabulous tool for identifying the shape of your distribution. So far, we've been looking at symmetric distributions, such as the normal distribution. Even so, not all distributions are symmetrical. You might have nonnormal data that are skewed.

The shape of the distribution is a fundamental characteristic of your sample that tin can determine which measure of primal trend best reflects the center of your data. Relatedly, the shape also impacts your option between using a parametric or nonparametric hypothesis test. In this manner, histograms are informative about the summary statistics and hypothesis tests that are appropriate for your information.

For skewed distributions, the direction of the skew indicates which style the longer tail extends.

For right-skewed distributions, the long tail extends to the right while most values cluster on the left, as shown beneath. These are real data from a written report I conducted.

Conversely, for left-skewed distributions, the long tail extends to the left while well-nigh values cluster on the right.

Related posts: The Normal Distribution in Statistics and Parametric vs. Nonparametric Hypothesis Tests

Using Histograms to Identify Outliers

Histograms are a handy style to identify outliers. In an instant, you'll see if there are any unusual values. If you identify potential outliers, investigate them. Are these data entry errors or practice they represent observations that occurred under unusual conditions? Or, mayhap they are legitimate observations that accurately describe the variability in the report area.

In a histogram, outliers appear as an isolated bar.

Related posts: v Ways to Discover Outliers and Guidelines for Removing Outliers

Identifying Multimodal Distributions with Histograms

A multimodal distribution has more than i pinnacle. Information technology's piece of cake to miss multimodal distributions when you focus on summary statistics, such equally the mean and standard deviations. Consequently, histograms are the best method for detecting multimodal distributions.

Imagine your dataset has the properties shown beneath.

That looks relatively straightforward, simply when yous graph it, you see the histogram beneath.

That bimodal distribution is not quite what y'all were expecting! This histogram illustrates why you should always graph your data rather than just calculating summary statistics!

Using Histograms to Place Subpopulations

Sometimes these multimodal distributions reverberate the actual distribution of the phenomenon that y'all're studying. In other words, at that place are genuinely different pinnacle values in the distribution of one population. However, in other cases, multimodal distributions indicate that you're combining subpopulations that have different characteristics. Histograms can help confirm the presence of these subpopulations and illustrate how they're different from each other.

Suppose we're studying the heights of American citizens. They accept a mean height of 168 centimeters with a standard deviation of 9.8 CM. The histogram is below. In that location appears to exist an unusually broad tiptop in the center—it's not quite bimodal.

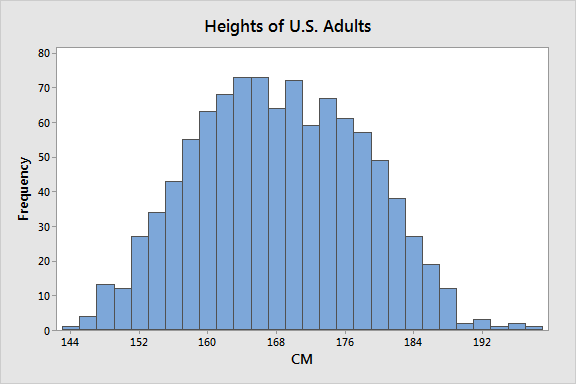
When we dissever the sample by gender, the reason for it becomes clear.

Notice how two narrower distributions have replaced the unmarried broad distribution? The histograms assistance us learn that gender is an essential categorical variable in studies that involve height. The graphs testify that the mean provides more precise estimates when we assess heights by gender. In fact, the hateful for the entire population does not equal the mean for either subpopulation. It's misleading!

Related mail: Dot Plots: Using, Examples, and Interpreting

Using Histograms to Assess the Fit of a Probability Distribution Role

Analysts tin overlay a fitted line for a probability distribution function on their histogram. Hither's a quick stardom between the 2:

• Histogram: Displays the distribution of values in the sample.
• Fitted distribution line: Displays the probability distribution function for a item distribution (e.g., normal, Weibull, etc.) that best fits your data.

A histogram graphs your sample data. On the other manus, a fitted distribution line attempts to find the probability distribution role for a population that has the maximum likelihood of producing the distribution that exists in your sample.

While you tin can use histograms to evaluate how well the distribution curve fits your sample, I do Not recommend it! If you insist on using a histogram, assess how closely the confined follow the shape of the fitted line. In the graph below, the fitted line for the normal distribution appears to follow the histogram bars adequately. The fable displays the estimated parameter values of the fitted distribution.

Instead of using histograms to determine how well a distribution fits your data, I recommend using a combination of distribution tests and probability plots. Probability plots are special graphs that are specifically designed to brandish how well probability distribution functions fit samples. To learn more most these other approaches, read my posts about Identifying the Distribution of your Data and Histograms vs. Probability Plots.

Related mail: Understanding Probability Distributions

Using Histograms to Compare Distributions betwixt Groups

To compare distributions between groups using histograms, you'll need both a continuous variable and a categorical grouping variable. There are two common ways to brandish groups in histograms. You tin can either overlay the groups or graph them in different panels, equally shown below.

It can exist easier to compare distributions when they're overlaid, only sometimes they become messy. Histograms in dissever panels display each distribution more conspicuously, but the comparisons and degree of overlap aren't quite equally clear. In the examples above, the paneled distributions are clearly more legible. However, overlaid histograms tin can work nicely in other cases, as you lot've seen in this blog post. Experiment to find the best approach for your data!

While I think histograms are the all-time graph for understanding the distribution of values for a single grouping, they can get muddled with multiple groups. Histograms are usually pretty good for displaying two groups, and up to iv groups if yous display them in dissever panels. If your primary goal is to compare distributions and your histograms are challenging to interpret, consider using boxplots or individual plots. In my opinion, those other plots are ameliorate for comparing distributions when y'all accept more groups. Just they don't provide quite as much detail for each distribution as histograms.

Over again, experiment and determine which graph works best for your data and goals!

Related post: Boxplots vs. Individual Value Plots: Graphing Continuous Data past Groups

Histograms and Sample Size

As fantastic as histograms are for exploring your information, be aware that sample size is a significant consideration when you lot need the shape of the histogram to resemble the population distribution. Typically, I recommend that you have a sample size of at least fifty per group for histograms. With fewer than 50 observations, yous take too little data to correspond the population distribution accurately.

Both histograms below use samples drawn from a population that has a mean of 100 and a standard deviation of 15. These characteristics describes the distribution of IQ scores. However, one histogram uses a sample size of 20 while the other uses a sample size of 100. Detect that I'm using percent on the Y-axis to compare histogram bars betwixt different sample sizes.

That'southward a pretty huge deviation! It takes a surprisingly large sample size to get a proficient representation of an entire distribution. When your sample size is less than 20, consider using an individual value plot.

Using Hypothesis Tests in Conjunction with Histograms

As y'all've seen in this post, histograms can illustrate the distribution of groups as well equally differences between groups. However, if you want to use your sample data to describe conclusions almost populations, yous'll need to use hypothesis tests. Additionally, be sure that you apply a sampling method, such as random sampling, to obtain a sample that reflects the population.

Related posts: Departure between Descriptive and Inferential Statistics and Populations, Parameters and Samples in Inferential Statistics

Differences between groups that are visible on histograms can be quirks acquired by random sampling mistake rather than representing real differences between populations. On histograms, random mistake can manifest itself as differences between fundamental tendency and variability. Additionally, arbitrary graph factors such as the scale of the Y-axis and unlike bin sizes can overstate the differences.

Hypothesis tests play a critical role in separating the betoken (real differences in the population) from the racket (random sampling error). This protective role helps prevent you from mistaking random error for a real effect. If the advisable hypothesis test is not statistically meaning, your sample provides insufficient show for concluding that the design on your graph represents a real effect at the population level. In other words, yous might be looking at dissonance in the sample.

Hypothesis Tests for Histograms

Use the following hypothesis tests in conjunction with histograms when yous are comparing groups:

ii-sample t-exam: Assess the equality of ii group ways.

ANOVA: Test the equality of 3 or more group means.

Mann-Whitney: Appraise the equality of two grouping medians.

Kruskal-Wallis and Mood's Median: Examination the equality of three or more group medians.

Examination of Equal Variances: Appraise the equality of group variances or standard deviations.

Histograms are a great way to investigate your data. Yet, when you need to draw inferences about an entire population, exist certain to apply a representative sampling method and the proper hypothesis exam.

Related post: Median: Definition and Uses

Source: https://statisticsbyjim.com/basics/histograms/

Posted by: terrellsuaing.blogspot.com

Share this post